Quantum K-Means

QKMeans Algorithm

class QKMeans(n_clusters=6, quantum_instance=None, *, init='kmeans++', n_init=1, max_iter=30, tol=0.0001, random_state=42)

Bases: sklearn.base.ClusterMixin, qlearnkit.algorithms.quantum_estimator.QuantumEstimator

The Quantum K-Means algorithm for classification

Note

The naming conventions follow the KMeans from sklearn.cluster

Example

Classify data using the Iris dataset.

import numpy as np
import matplotlib.pyplot as plt
from qlearnkit.algorithms import QKMeans
from qiskit import BasicAer
from qiskit.utils import QuantumInstance, algorithm_globals
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

seed = 42
algorithm_globals.random_seed = seed

quantum_instance = QuantumInstance(BasicAer.get_backend('qasm_simulator'),
                                   shots=1024,
                                   optimization_level=1,
                                   seed_simulator=seed,
                                   seed_transpiler=seed)

# Use iris data set for training and test data
X, y = load_iris(return_X_y=True)

num_features = 2
X = np.asarray([x[0:num_features] for x, y_ in zip(X, y) if y_ != 2])
y = np.asarray([y_ for x, y_ in zip(X, y) if y_ != 2])

qkmeans = QKMeans(n_clusters=3,
                  quantum_instance=quantum_instance
)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=seed)
qkmeans.fit(X_train)

print(qkmeans.labels_)
print(qkmeans.cluster_centers_)

# Plot the results
colors = ['blue', 'orange', 'green']
for i in range(X_train.shape[0]):
    plt.scatter(X_train[i, 0], X_train[i, 1], color=colors[qkmeans.labels_[i]])
plt.scatter(qkmeans.cluster_centers_[:, 0], qkmeans.cluster_centers_[:, 1], marker='*', c='g', s=150)
plt.show()

# Predict new points
prediction = qkmeans.predict(X_test)
print(prediction)

[0 0 2 1 0 2 2 0 1 0 1 1 2 2 0 2 0 0 1 2 1 1 2 0 2 2 0 1 0 1 1 1 2 1 1 0 1
 0 2 0 0 0 0 2 2 0 2 0 0 0 0 1 0 2 1 1 0 2 0 1 0 0 2 1 1 0 2 1 2 0 0 0 0 0
 2 0 0 2 0 0]
[[5.96216216 2.77027027]
 [4.74761905 3.02857143]
 [5.34090909 3.63181818]]

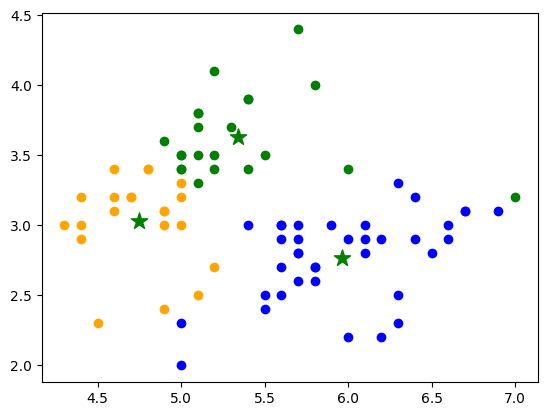
[0 0 0 1 2 2 2 0 2 2 2 1 0 2 0 2 0 0 1 2]

Parameters

• n_clusters – The number of clusters to form as well as the number of centroids to generate.

• quantum_instance – the quantum instance to set. Can be a QuantumInstance or a Backend

• init – Method of initialization of centroids.

• n_init – Number of time the qkmeans algorithm will be run with different centroid seeds.

• max_iter – Maximum number of iterations of the qkmeans algorithm for a single run.

• tol – Tolerance with regard to the difference of the cluster centroids of two consecutive iterations to declare convergence.

• random_state – Determines random number generation for centroid initialization.

fit(X, y=None)

Fits the model using X as training dataset and y as training labels. For the qkmeans algorithm y is ignored. The fit model creates clusters from the training dataset given as input

Parameters

• X – training dataset

• y – Ignored. Kept here for API consistency

Returns

trained QKMeans object

predict(X_test)

Predict the labels of the provided data.

Parameters

X_test – ndarray, test samples

Return type

ndarray

Returns

Index of the cluster each sample belongs to.

score(X, y=None, sample_weight=None)

Returns Mean Silhouette Coefficient for all samples.

Parameters

• X – array of features

• y – Ignored. Not used, present here for API consistency by convention.

• sample_weight – Ignored. Not used, present here for API consistency by convention.

Return type

float

Returns

Mean Silhouette Coefficient for all samples.

QKMeans Circuit

construct_circuit(input_point, centroids, k)

Apply a Hadamard to the ancillary qubit and our mapped data points. Encode data points using U3 gate. Perform controlled swap to entangle the state with the ancillary qubit Apply another Hadamard gate to the ancillary qubit. .. parsed-literal:

        ┌───┐                   ┌───┐
|0anc>: ┤ H ├────────────■──────┤ H ├────────M
        └───┘            |      └───┘
        ┌───┐   ┌────┐   |
|0>: ───┤ H ├───┤ U3 ├───X──────────
        └───┘   └────┘   |
        ┌───┐   ┌────┐   |
|0>: ───┤ H ├───┤ U3 ├───X──────────
        └───┘   └────┘

Parameters

• input_point – Input point from which calculate the distance.

• centroids – Array of points representing the centroids to calculate the distance to

• k – Number of centroids

Return type

QuantumCircuit

Returns

The quantum circuit created

Initializations

random(X, n_clusters, random_state=42)

Create random cluster centroids.

Parameters

• X – The dataset to be used for centroid initialization.

• n_clusters – The desired number of clusters for which centroids are required.

• random_state – Determines random number generation for centroid initialization.

Return type

ndarray

Returns

Collection of k centroids as a numpy ndarray.

kmeans_plus_plus(X, k, random_state=42)

Create cluster centroids using the k-means++ algorithm.

Parameters

• X – The dataset to be used for centroid initialization.

• k – The desired number of clusters for which centroids are required.

• random_state – Determines random number generation for centroid initialization.

Return type

ndarray

Returns

Collection of k centroids as a numpy ndarray.

naive_sharding(X, k)

Create cluster centroids using deterministic naive sharding algorithm.

Parameters

• X – The dataset to be used for centroid initialization.

• k – The desired number of clusters for which centroids are required.

Return type

ndarray

Returns

Collection of k centroids as a numpy ndarray.